Material referido a clases - Procesamiento digital de señales

Procesamiento digital de señales

Transformada discreta de cosenos (DCT)

La información mas completa está en la página sobre Discrete Cosine Transform en Wikipedia. La forma de la DCT mas popular es el tipo II, tal como utilizado en archivos de imágenes del tipo JPEG.

Por desgracia, el ejemplo en esta página es poco felíz: El fuerte de DCT no es exactamente la compresión de elementos como caracteres o dibujos técnicos. Por este motivo, adjunto una serie de imágenes que indican propiedades de la DCT.

Introducción

Una imagen, antes de producirse el archivo JPEG, es sometida a varios pasos:

Conversión de RGB a YCbYr (La parte Cr y Cb (Crominancia) tiene la información de color de la imagen. 'Y' es la luminancia. Crominancia puede compactarse mucho mas que Luminancia antes de que el ojo se dé cuenta.
Compactación con DCT
La salida de la DCT puede reducirse notablemente leyendo los coeficientes en forma diagonal (ver el artículo en Wikipedia).

En DCT-II, tal como utilizada en JPEG, la imagen original es subdividida en bloque(cito)s de 8 por 8 pixeles. Cada bloque se procesa con la DCT por separado.

Ya que los valores originales se expresan de 0 a 255, para evitar una componente muy grande de 'DC', se 'resta' 128 de cada byte de la imagen original (resultando en valores de -128 a +128).

Sobre las funciones base utilizadas en DCT

Tal como vimos en la transformada de Fourier, podemos hacer la DCT mediante correlación de funciones base precalculadas. Si deseamos hacer la DCT en 2D, podemos hacer primero la DCT de una dimensión sobre cada fila de la imagen y, sobre el resultado, la DCT de 1D sobre cada columna de pixeles.

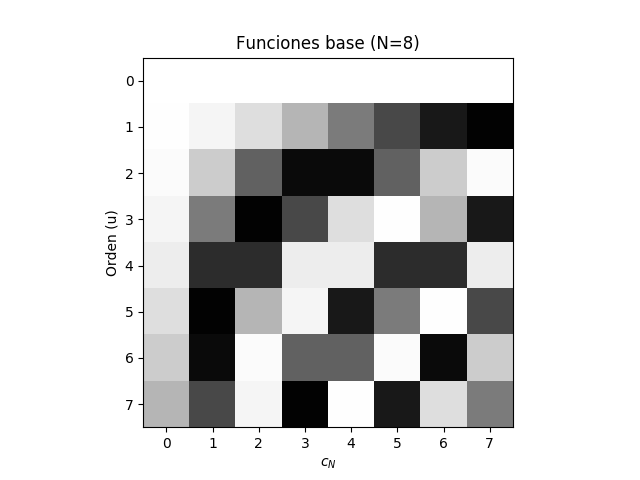
Esta imagen muestra los valores de las 8 funciones bases necesarias para una DCT de 1D sobre una línea de 8 pixeles. La fila 0 indica los coeficientes de la primera función base (todos 1, o blanco).

Como primer paso, podemos aplicar estas funciones base sobre cada file. En la imagen se repiten las funciones base file por file.

Luego, podemos hacer lo mismo columna por columna.

O, podemos combinar los dos paso, aplicando las bases verticales sobre las horizantales, obteniendo un total de 64 funcines base diferentes.

Un par de pruebas con imágenes básicas

Imagen original gris 50%

Probemos con una imagen sencilla. Todos los pixeles tienen color gris de 50%. Recuerden, este valor corresponde con 128 en la escala de 0 a 255.
Por otro lado, restaremos 128 en el algoritmo, para eleminar este componente de 'continua'.

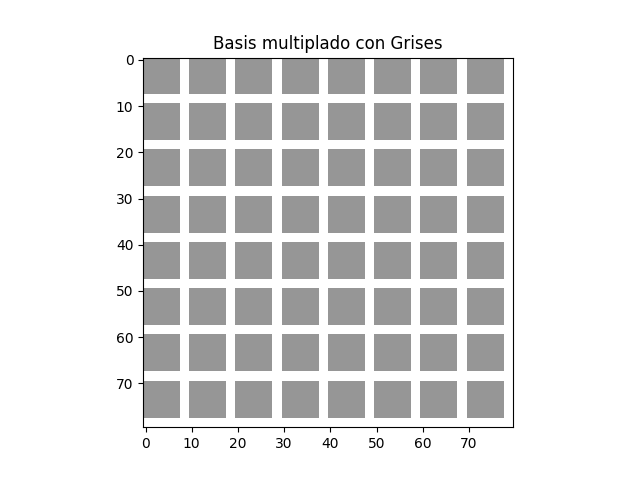
Multiplicamos cada función base con la imagen de entrada (gris). Ya que cada pixel de la imagen corresponde con el valor Cero, el resultado consiste de 64 imagenes grises.

Imagen original gris 56%

Si aumentamos un poco la intensidad del gris (de 50 a 56%), tendriamos que obtener un resultado mas significativo.

Multiplicando de nuevo con las funciones base, notamos que aparecen los primeros signos de componentes.

Sumando todos los pixeles de cada multuplicación, obtenemos los coeficientes (o el 'resultado' de la transformada). Aquí notamos ún solo coeficiente (arriba, a la izquierda) que no es cero, indicando que no hay componentes superiores - solo 'continua'.
Indica también, que el bloquecito de 8x8 que analizamos, se puede representar por un solo valor!

Ahora con una imagen real

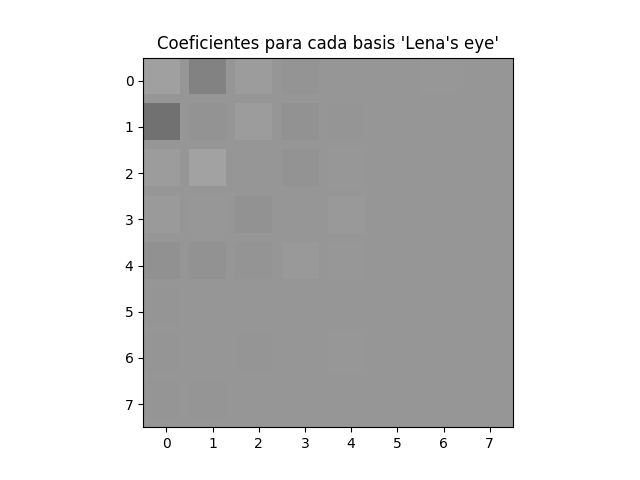
Esta imagen es un detalle de la pupila de un ojo. Es mas representativo de una fracción de una foto típica que se encuentra en formato JPEG.

Nuevamente, aplicamos la multiplcación con las funciones base, y obtenemos la imagen a la izquierda...

luego de promediar los pixeles en cada producto, notamos que solo unos pocos pixeles se distinguen del color gris del fondo. De nuevo, si eliminamos todos los pixele sin información, se reduce el tamaño notablemente.

Para comparación, sique aquí el ejemplo de Wikipedia.

Esta es la 'A' que trataremos de pasar por la DCT.

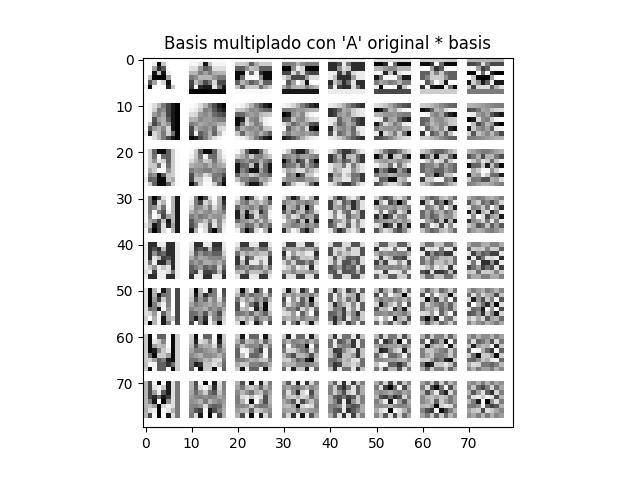
Como de costumbre, multiplicamos por las funciones base.

Como resultado de que esta figura (la 'A') contiene contrastes altos, la imagen tiene relativamente mucho mas coeficientes que no son despreciable. Reducción de la cantidad de coeficientes para compresión tendrá efectos muy notables en la imagen final.

Efectos de la calidad en imágenes JPG

Em lo que sigue un ejemplo de los efectos utilizar al formato jpg para dibujos con muchos detalles (o el porque no aconsejable utilizar jpg para imágenes técnicos).
Para el demo, se hizo un pequeño dibujo (100 por 100 píxeles) con detalles de alto contraste.
Luego se guardó la imagen con diferentes calidades (1, 2, 5, 10 y otros) y se muestra una ampliación con los cuadros de 8x8 utilizados en la transformada de cosenos.

Imagen jpg	Ampliación y división en 8x8	Tamaño
Imagen original, formato png.		1620 bytes
jpg calidad 80%.		7192 bytes
jpg calidad 50%.		2092 bytes
jpg calidad 20%.		6344 bytes
jpg calidad 10%.		6187 bytes
jpg calidad 5%		6080 bytes
jpg calidad 2%.		6010 bytes
jpg calidad 1%.		6010 bytes

Mas información

Youtube video sobre JPEG	Video interesante sobre todo el proceso de compresion con DCT en JPEG. La persona hable relativamente rápido, pero el video tiene la posibilida de subtítulos y de reproducción lenta.
Página en Wikipedia	Página bien redactada en Wikipedia
dct en Scipy	Página de referencia de la función dct() tal como implementada en Scipy)
Discrete Cosine Transform	PDF con un paper de Gilbert Strang - muy detallado, con algunos algoritmos e ideas para aumentar la velocidad.
What are wavelets? (1) What are wavelets? (2) What are wavelets? (3) What are wavelets? (4)	Serie de 4 video tutoriales sobre wavelets de MathWorks

1694

correo

	Esta imagen muestra los valores de las 8 funciones bases necesarias para una DCT de 1D sobre una línea de 8 pixeles. La fila 0 indica los coeficientes de la primera función base (todos 1, o blanco).
	Como primer paso, podemos aplicar estas funciones base sobre cada file. En la imagen se repiten las funciones base file por file.
	Luego, podemos hacer lo mismo columna por columna.
	O, podemos combinar los dos paso, aplicando las bases verticales sobre las horizantales, obteniendo un total de 64 funcines base diferentes.

	Probemos con una imagen sencilla. Todos los pixeles tienen color gris de 50%. Recuerden, este valor corresponde con 128 en la escala de 0 a 255. Por otro lado, restaremos 128 en el algoritmo, para eleminar este componente de 'continua'.
	Multiplicamos cada función base con la imagen de entrada (gris). Ya que cada pixel de la imagen corresponde con el valor Cero, el resultado consiste de 64 imagenes grises.

	Si aumentamos un poco la intensidad del gris (de 50 a 56%), tendriamos que obtener un resultado mas significativo.
	Multiplicando de nuevo con las funciones base, notamos que aparecen los primeros signos de componentes.
	Sumando todos los pixeles de cada multuplicación, obtenemos los coeficientes (o el 'resultado' de la transformada). Aquí notamos ún solo coeficiente (arriba, a la izquierda) que no es cero, indicando que no hay componentes superiores - solo 'continua'. Indica también, que el bloquecito de 8x8 que analizamos, se puede representar por un solo valor!

	Esta imagen es un detalle de la pupila de un ojo. Es mas representativo de una fracción de una foto típica que se encuentra en formato JPEG.
	Nuevamente, aplicamos la multiplcación con las funciones base, y obtenemos la imagen a la izquierda...
	luego de promediar los pixeles en cada producto, notamos que solo unos pocos pixeles se distinguen del color gris del fondo. De nuevo, si eliminamos todos los pixele sin información, se reduce el tamaño notablemente.

	Esta es la 'A' que trataremos de pasar por la DCT.
	Como de costumbre, multiplicamos por las funciones base.
	Como resultado de que esta figura (la 'A') contiene contrastes altos, la imagen tiene relativamente mucho mas coeficientes que no son despreciable. Reducción de la cantidad de coeficientes para compresión tendrá efectos muy notables en la imagen final.