Material referido a clases - Computación IV

Generación de audio con un microcontrolador

La generación de audio se hace en tres pasos:

1) Conversión de la imagen a 'pixels', y determinar la frecuencia necesaria para enviar este nivel.

2) Según la necesidad de 1), se calcula, en intervalos constantes, el incremento de fase de la senusoide de salida, necesario para la frecuencia requerida

3) Mediante una tabla, se convierte la fase de 2) en la forma de onda a transmitir

La parte de conversión de la imagen se hace en otra página. en lo que sigue describo el mecanismo de generación de audio.

Cálculo del incremento de fase

Ya que no disponemos de cálculos de punto flotante en nuestro controlador, tenemos que buscar una forma de hacer el cálculo con 8 bits. No hay instrucciones de multiplicaciones, entonces por el reducido tiempo disponible, todos los cáculos se debe limitar a sumas/restas!

En lo que sigue, suponemos (con bastante buen criterio) que la frecuencia de actualización de la señal de salida será 10 kHz, y que la tabla de la senusoide tendrá 32 entradas ('lookup-table').

Frecuencia Período NroMuest PasoTabla

Fsinc 1200 0.0008333 8.3333 3.84

Fnegro 1500 0.0006667 6.6667 4.8

Fgris 1900 0.0005263 5.3632 6.08

Fblanco 2300 0.0004348 4.3478 7.36

En la tabla vemos para diferentes frecuencias a generar, cual es el período correspondiente, y luego cuantos 'intervalos' de 10kHz eso significa.

Ya que la tabla tiene 32 valores, podemos calcular cual es el 'incremento de fase' necesario, expresado en 'pasos en la tabla'. Claro que no podemos incremente un puntero 3.84 lugares, tendremos que incrementarlo 3 o 4. Eso introduce momentáneamente un error de fase, que lo podemos corregir en siguientes pasos, si nos acordamos de la parte decimal. Como implementar esto en una forma compacta?

El incremento mínimo parece de 3.84, el máximo de 5.44. Si lo consideramos, el valor máximo es menos de 8, asi que lo podemos codificar con 3 bits. Si usamos los 3 más significativos de un byte, y los 5 restantes para la parte 'decimal', logramos ya una precisión aceptable:

Frecuencia Período PasoTabla dFase FreqLograda

Fsinc 1200 0.0008333 3.84 123 1201.17

Fnegro 1500 0.0006667 4.8 154 1503.91

Fgris 1900 0.0005263 6.08 195 1904.30

Fblanco 2300 0.0004348 7.36 236 2304.69

El error en todos los casos es menos de 0.3%! No está mal para un algoritmo tan sencillo. Sin embargo, variando un poco los parámetros podemos ganar aún mejor calidad, con muy poco costo en términos de programación. Considermos que siempre hay que sumar 3 (de 3.84), entonces podemos codificar la suma del '3' fijo en las rutinas, y restar 3 de la columna 'PasoTabla'. El valor máximo ahora es 7.36 - 3 = 4.36. Todavía necesitamos 3 bits para codificar el 4, así que no ganamos nada.

Pero si modificamos un poco la frecuencia de muestreo (aumentar), entonces podemos bajar el valor, sin que 3.84 baje de 3. Con 11905 Hz de muestreo (1 MHz/84):

Frecuencia Período PasoTabla -3 dFase FreqLograda

Fsinc 1200 0.0008333 3.226 0.226 14 1197.48

Fnegro 1500 0.0006667 4.032 1.032 66 1499.75

Fgris 1900 0.0005263 5.107 2.107 135 1900.85

Fblanco 2300 0.0004348 6.182 3.182 204 2301.94

Ahora necesitamos solo 2 bits para el incremento, y nos quedan 6 bits para la parte decimal. El error máximo bajó a 0.2%, pero quizás aún más importante, tenemos un rango de 66 a 204 para variar los tonos de la imagen, o sea, 138 niveles de grises que se pueden representar. En el caso anterior, habia solo 82 niveles de grises.

Lo único que tenemos que hacer, es reprogramar el timer del PIC para generar los 11905 Hz, y no olvidarse de sumar 3 a cada incremento del offset en la tabla.

El algoritmo de generación del audio será entonces:

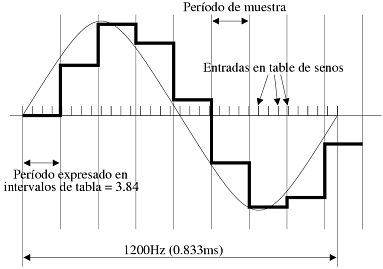
Considerando que tenemos un registro del PIC donde sera depositado dFase (según la necesidad de la imagen):: - Sincronizar con 11905 Hz (interrupt?); - Tomar el puntero a la tabla calculada anteriormente y enviar el valor al puerto de salida.; - Sumar 3 a la Fase (el valor fijo); - Sumar dFase al acumulador de fase, si hay CY, sumar 1 al puntero; - Sumar los dos bits mas significativos del acumulador al puntero

Sigue un gráfico que intenta aclara el mecanismo. Este gráfico está creado con frecuencia de muestreo de 10 kHz.

Y abajo un gráfico de la señal generada, considerando que la tabla tiene simplemente un senos codificado con 3 bits (bloques color violeta). Al lado (azúl), está el valor correcto (calculado con el senos exacto). Se puede notar que el resultado es bastante bueno! Con las funciones de Walsh tendría que mejorar algo mas todavía.

Aqui un ejemplo de la generación de 1900 Hz:

Paso    Accu	Carry	AccuR	Ptr
0	0	0	0	0
1	135	0	135	5
2	270	1	14	9
3	405	0	149	14
4	540	1	28	18
5	675	0	163	23
6	810	1	42	27
7	945	0	177	0
8	1080	1	56	4
9	1215	0	191	9
10	1350	1	70	14
11	1485	0	205	20
12	1620	1	84	25
13	1755	0	219	31
14	1890	1	98	4
15	2025	0	233	10
16	2160	1	112	15
17	2295	0	247	21
18	2430	1	126	26
19	2565	1	5	30
20	2700	0	140	3

Accu:: El acumulador donde se van sumando los 135 (dFase). Aquí es no es el valor real, ya que se trabaja con 8 bits, el valor no puede superar los 255. Eso se refleja en la columna AccuR. Cada vez que se supera los 255, se genera un Carry, que hay que sumar también.
Carry:: El carry que se genera cuando AccuR + dFase (aqui 135) supera los 255
AccuR:: El valor real del registro Accu (limitado a 0..255)
Ptr:: El puntero que va recorriendo la tabla de senos. Cada paso, se suma el Carry, la constante 3 (recuerden?) y los dos bits mas significativos del AccuR.

Vinculos relacionados a la generación de audio

Vínculo	Idioma	Descripción	Fuente
Walsh functions: A digital Fourier series	Inglés	Funciones de Walsh: Muy buen artículo	John
Applications of Walsh Functions in Communications	Inglés	Aplicaciones de funciones de Walsh en comunicaciones	John

correo

	Frecuencia	Período	NroMuest	PasoTabla
Fsinc	1200	0.0008333	8.3333	3.84
Fnegro	1500	0.0006667	6.6667	4.8
Fgris	1900	0.0005263	5.3632	6.08
Fblanco	2300	0.0004348	4.3478	7.36